
गोल्डन रेशियो के उदाहरण क्लासिक वास्तुकला, कलाकृति, प्रकृति और यहां तक कि संगीत में हर जगह पाए जा सकते हैं। अनुपात की यह अभिव्यक्ति, जिसे दैवीय अनुपात के रूप में भी जाना जाता है, प्राकृतिक और मानव निर्मित दोनों तरह के डिजाइन में एक अपरिमेय संख्या (1.618) के अनुप्रयोग के माध्यम से सामंजस्यपूर्ण रचना प्रदान करती है। सबसे अधिक संभावना है, आप गोल्डन रेशियो की सुंदरता के पीछे के गणित से अनजान हैं क्योंकि यह ऐसी वस्तुओं और संगीत का उत्पादन करता है जो आपको बिना किसी स्पष्टीकरण की आवश्यकता के स्वाभाविक रूप से सुखद लगेगा।
वास्तुकला में स्वर्णिम अनुपात
गोल्डन रेशियो प्रकृति और कला में लगभग पूर्ण सुंदरता पैदा करता है। जब आप रोजमर्रा की जिंदगी में गोल्डन रेशियो के उदाहरण ढूंढना शुरू करते हैं, तो आप यह देखकर आश्चर्यचकित हो सकते हैं कि इसका उपयोग कई स्मारकीय इमारतों और संरचनाओं को बनाने के लिए किया गया है। जब वास्तुकला में स्वर्ण अनुपात का उपयोग किया जाता है, तो कहा जाता है कि इमारत "पवित्र वास्तुकला" का उपयोग करके बनाई गई है। एक वर्ग पर सुनहरे अनुपात की गणना लागू करके, आर्किटेक्ट और डिजाइनर गोल्डन रेक्टेंगल बनाने में सक्षम होते हैं, जिसके बारे में माना जाता है कि इसका अनुपात मानव आंख के लिए सबसे सौंदर्यपूर्ण रूप से सुखद है।
गोल्डन रेक्टेंगल उदाहरण: पार्थेनन

फिडियास, ग्रीक मूर्तिकार, ने अपने काम में गोल्डन रेशियो का उपयोग किया, खासकर जब उन्होंने पार्थेनन स्तंभों के ठीक ऊपर बनाए गए बैंड के साथ काम करना शुरू किया। यह भी ध्यान रखना महत्वपूर्ण है कि गोल्डन रेशियो, फी को दिए गए संख्यात्मक मान को उनके सम्मान में नामित किया गया था।
यदि आप पार्थेनन के बाहरी हिस्से के आयामों को मापते हैं, तो आप पाएंगे कि यह न केवल एक सुनहरा आयत बनाता है, बल्कि स्तंभों के बीच कई सुनहरे आयत भी हैं। यह पवित्र संरचना वास्तुकला में स्वर्णिम अनुपात का एक सुंदर उदाहरण है।
स्वर्ण त्रिभुज उदाहरण: गीज़ा का महान पिरामिड
गोल्डन रेशियो, गोल्डन रेक्टेंगल और गोल्डन ट्राइएंगल सभी दुनिया के सात अजूबों में से एक, गीज़ा के महान पिरामिड की पूर्णता में पाए जा सकते हैं। स्वर्णिम अनुपात ज्ञात करने के लिए, आपको पिरामिड के वर्गाकार आधार को आधा करना होगा और पिरामिड के केंद्र तक एक ऊर्ध्वाधर रेखा खींचनी होगी। जब इसे पिरामिड के कोणीय पक्ष से जोड़ा जाता है, तो आप आसानी से देख सकते हैं कि यह 1.618 अनुपात, स्वर्ण अनुपात के साथ स्वर्ण त्रिभुज कैसे बनाता है।
अन्य वास्तुशिल्प उदाहरण
आप प्राचीन से आधुनिक पवित्र वास्तुकला और गोल्डन रेशियो इमारतों के कई उदाहरण पा सकते हैं।
- चार्ट्रेस कैथेड्रल - सेंटर, फ़्रांस
- नोट्रे डेम - पेरिस, फ़्रांस
- पोर्च ऑफ मेडेंस - एक्रोपोलिस, एथेंस
- ताजमहल - आगरा, भारत
- संयुक्त राष्ट्र भवन - न्यूयॉर्क शहर, न्यूयॉर्क
कला उदाहरणों में स्वर्णिम अनुपात
आप गोल्डन रेशियो का उपयोग करने वाले मास्टर चित्रकारों के कई उदाहरण पा सकते हैं। उत्कृष्टता के ये कार्य स्वर्ण आयतों और स्वर्ण त्रिभुजों के अनुपात का उपयोग करके बनाए गए थे। गोल्डन रेक्टेंगल के आधार पर बनाई गई कला मानव आंखों के लिए अधिक सुखदायक साबित होती है। यह उन रहस्यों में से एक है जो इस पूर्ण आयत और स्वर्णिम अनुपात से घिरा हुआ है।
कला में स्वर्णिम अनुपात

स्वर्ण अनुपात कला उदाहरणों में शामिल हैं:
- लियोनार्डो डि विंची - मोना लिसा, विट्रुवियन मैन
- बॉटीसेली - शुक्र का जन्म
- माइकल एंजेलो - पवित्र परिवार, 'डेविड'
- राफेल - सूली पर चढ़ना
- रेम्ब्रांट - सेल्फ़-पोर्ट्रेट
- साल्वाडोर डाली - अंतिम भोज का संस्कार, स्मृति की दृढ़ता
कला रचना में स्वर्णिम अनुपात का उपयोग
गोल्डन रेक्टेंगल के भीतर कुछ ऐसे क्षेत्र हैं जो अन्य क्षेत्रों की तुलना में अधिक आकर्षक पाए जाते हैं। इन बिंदुओं को आयत के निचले कोने से विपरीत कोने तक एक रेखा खींचकर और इसे दूसरे निचले कोने के साथ दोहराकर खोजा जाता है। ये रेखाएँ स्वर्ण आयत के ठीक केंद्र पर प्रतिच्छेद करेंगी। इसके बाद, केंद्र बिंदु से शुरू करते हुए प्रत्येक पंक्ति के मध्य को मापें। इन चार बिंदुओं को आयत की आंखें (गोल्डन रेशियो) कहा जाता है। पेंटिंग का मुख्य केंद्र बिंदु तब रुचि के इन बिंदुओं (अनुपातों) के भीतर खींचा या चित्रित किया जाता है।
संगीत में सुनहरा अनुपात

संगीत संख्यात्मक मूल्य से बना है और जब संगीतमय टुकड़ा बनाने के लिए गोल्डन रेशियो का उपयोग किया जाता है, तो यह गणित का एक जीवंत उदाहरण बन जाता है। फाइबोनैचि अनुक्रम संगीत में भी प्रचलित है:
- एक पैमाने में आठ नोट होते हैं.
- तीसरा और पांचवां स्वर स्वरों का आधार हैं।
- किसी भी नोट की लंबाई, या सप्तक, 13 नोट है।
संगीत के एक टुकड़े के दौरान अनुक्रम जारी रहता है और स्वर्णिम अनुपात तक पहुंचने पर यह और अधिक जटिल हो जाता है।
गोल्डन रेशियो का उपयोग करने वाले संगीतकार
कुछ सबसे प्रसिद्ध शास्त्रीय संगीतकारों ने अपने संगीत टुकड़ों में गोल्डन रेशियो और फाइबोनैचि अनुक्रमण का उपयोग किया, जिनमें बाख, बीथोवेन, चोपिन और मोजार्ट शामिल हैं। केसी मोंगोवन जैसे कुछ आधुनिक संगीतकारों ने अपने संगीत में स्वर्णिम अनुपात की खोज की है।
प्रकृति में सुनहरे अनुपात के उदाहरण

स्वर्णिम अनुपात प्रकृति में कहाँ पाया जाता है? यह गोल्डन या फाइबोनैचि सर्पिल में है, जिसे गोल्डन रेशियो का उपयोग करके बनाया जा सकता है। यह एक ऐसी घटना है जो प्राकृतिक दुनिया में बड़े पैमाने पर पाई जाती है। एक पौधे की पत्तियाँ इतनी बढ़ती हैं कि जितना संभव हो सके उतनी अधिक संख्या में तने पर चढ़ सकें। एक नया पत्ता एक के आगे बढ़ने के बाद ही बनता है।
- सर्पिल कैक्टि
- सर्पिल आकाशगंगाएँ
- सूरजमुखी
फाइबोनैचि अनुक्रम वाले फूल
कुछ फूलों में फूल की पंखुड़ियाँ होती हैं जो फाइबोनैचि अनुक्रम का पालन करती हैं:
- तीन पंखुड़ियाँ:आइरिस, लिली, ऑर्किड, ट्रिलियम
- पांच पंखुड़ियां: बटरकप, जेरेनियम, हिबिस्कस, सुबह की महिमा, नास्टर्टियम
- आठ पंखुड़ियाँ: डेल्फीनियम
- 13 पंखुड़ियाँ: डेज़ी, रैगवॉर्ट, गेंदा की कुछ किस्में
पाइनकोन्स में फाइबोनैचि सर्पिल

पेड़ की प्रजातियों के आधार पर, आप पाइनकोन में फाइबोनैचि संख्या श्रृंखला के भीतर गोल्डन रेशियो को काम करते हुए भी देख सकते हैं। आप पाइनकोन के एक तरफ आठ सर्पिलों की एक श्रृंखला पा सकते हैं, दूसरी तरफ 13 सर्पिलों के साथ। एक अन्य पाइनकोन पैटर्न में एक तरफ पांच सर्पिल और दूसरी तरफ आठ सर्पिल हैं।
मनुष्यों में स्वर्णिम अनुपात
यह अनुपात न केवल मनुष्य एक-दूसरे को कैसे देखते हैं, बल्कि उनके शरीर कैसे काम करते हैं, और उनके डीएनए में भी महत्वपूर्ण है।
DNA ने स्वर्णिम अनुपात का खुलासा किया
गोल्डन रेशियो का सबसे अद्भुत उदाहरण मानव डीएनए संरचना में पाया जाता है। इसे एकल डीएनए क्रॉस सेक्शन में देखा जा सकता है जिससे पता चलता है कि डीएनए डबल हेलिक्स एक दशमांश आकार बनाता है। यह दो पंचकोणों का संयोजन है, जो एक दूसरे से 36 डिग्री पर घूमते हैं, डीएनए डबल हेलिक्स बनाते हैं।डबल हेलिक्स सर्पिल स्वयं एक पंचकोण बनाता है। यहां तक कि एक डीएनए अणु भी स्वर्ण खंड या दिव्य अनुपात का आधार बताता है।
स्वर्णिम अनुपात के पीछे का गणित
वास्तविक जीवन में स्वर्णिम अनुपात खोजना सरल है, क्योंकि यह आपके चारों ओर दिखाई देता है। यह एक गणितीय सत्यवाद है जिसका उपयोग यह परिभाषित करने के लिए किया जाता है कि जिसे आमतौर पर प्रकृति में पाई जाने वाली पूर्ण संख्या के रूप में जाना जाता है, जिसे सदियों से मनुष्यों द्वारा दोहराया और अनुकरण किया गया है। इस संख्या की सरलीकृत सुंदरता इसके क्रियान्वयन की जटिलता को छिपा देती है। स्वर्णिम अनुपात के पीछे के सिद्धांत को समझने के लिए, आपको पहले अनुपात की फाइबोनैचि अनुक्रमण का पता लगाना होगा।
फाइबोनैचि अनुक्रम और स्वर्णिम अनुपात
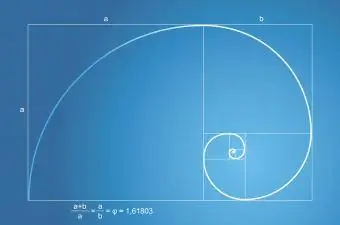
फाइबोनैचि अनुक्रम या श्रृंखला का स्वर्ण अनुपात से संबंध है। फाइबोनैचि श्रृंखला एक पौधे पर पत्तियों की संख्या और एक फूल पर पंखुड़ियों की संख्या को दर्शाती है।फाइबोनैचि सर्पिल, जो प्रकृति में पाया जाता है, हमेशा सुनहरे अनुपात के साथ एक सुनहरे आयत का हिस्सा होता है।
फाइबोनैचि श्रृंखला का गणित सरल है:
- क्रम 0 और 1 से शुरू होता है.
- श्रृंखला में अगला नंबर प्राप्त करने के लिए बस अंतिम दो संख्याओं को एक साथ जोड़ें।
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, इत्यादि।
- यह फाइबोनैचि श्रृंखला उदाहरण बन जाता है: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, इत्यादि।
फाइबोनैचि का स्वर्णिम अनुपात से संबंध तब साकार होता है जब इसे आगे, आगे, और आगे जोड़ा जाता है। आप जितनी अधिक श्रृंखला जोड़ेंगे, आप सुनहरे अनुपात के उतने ही करीब पहुंचेंगे।
एक सुनहरा आयत और त्रिभुज बनाना
फाइबोनैचि अनुक्रम के साथ एक सुनहरा आयत बनाने के लिए, आप एक वर्ग से शुरू करते हैं। आप मूल वर्ग में एक और वर्ग जोड़कर एक आयत बनाना शुरू करेंगे। सूत्र का उपयोग करना याद रखें: 0+1=1 पहला वर्ग है, 1+1=2 - आप एक और वर्ग जोड़ेंगे।1+2=3 आप तीन वर्ग जोड़ेंगे और अगले, 2+3=5, आप पांच वर्ग जोड़ेंगे। आप वर्ग जोड़ना जारी रखेंगे और अंततः एक सुनहरा आयत बनाएंगे।
एक स्वर्ण आयत को एक कोने से विपरीत कोने तक विभाजित करके एक स्वर्ण त्रिभुज बनाया जा सकता है। यह एक त्रिभुज बनाता है जहां इसकी तीन भुजाओं या कोणों का अनुपात 2:2:1 होता है, जिसका अर्थ है कि दो लंबी भुजाओं की लंबाई बराबर होती है और छोटा कोण दो लंबी भुजाओं की लंबाई का ठीक आधा होता है।
वास्तविक दुनिया में सुनहरा अनुपात
गोल्डन रेशियो को अक्सर प्रकृति और मानव शरीर में इसकी प्रमुखता के कारण दैवीय अनुपात के रूप में जाना जाता है। यह खोज कि स्वर्ण अनुपात कई जीवित चीजों में मौजूद है, इस जादुई अनुपात के प्रति श्रद्धा पैदा हुई, और यह आज भी कलाकारों और रचनाकारों के लिए प्रेरणा बनी हुई है।






